xxyQwQ
0%

【文章】从零开始实现支持向量机

发表于 更新于 分类于

写在前面

这篇文章诞生于机器学习课程无聊的大作业，既然已经为此浪费了不少时间，不妨再多花点时间写一篇文章，借此记录一下实现过程。支持向量机的数学形式简约而直观，但一旦涉及具体实现，各种问题就会接踵而来。在本文中，笔者将首先推导SVM的主要公式，接着基于Platt-SMO算法，从零开始实现支持多种核函数的SVM，然后基于One-Versus-One策略实现多分类，最后在MNIST和CIFAR-10数据集上进行性能测试

数学推导

基本形式

给定一个训练集 $\mathcal{D} = \{(\boldsymbol{x}_i, y_i)\}_{i=1}^m$，其中 $\boldsymbol{x}_i \in \mathbb{R}^n$ 是特征向量，$y_i \in \{+1, -1\}$ 是标签。线性SVM期望找到一个超平面 $\boldsymbol{w}^T \boldsymbol{x} + b = 0$，将正样本和负样本分开，其中 $\boldsymbol{w} \in \mathbb{R}^n$ 是法向量，$b \in \mathbb{R}$ 是偏移量

对于任一样本 $\boldsymbol{x}_i$，其到超平面的距离为

假定该超平面能将正负样本完全分开，即对于任一样本 $\boldsymbol{x}_i$有

注意到有一些样本满足 $\boldsymbol{w}^T \boldsymbol{x}_i + b = \pm 1$，它们被称为支持向量。支持向量到超平面的距离被称为间隔，记为

我们的目标是最大化间隔，即最小化 $\left|\boldsymbol{w}\right|$。因此，优化问题可以表述为

然而，这些样本并不总是线性可分的，因此我们引入Hinge损失函数

于是，优化问题可以表述为

如果我们引入松弛变量 $\xi_i \geq 0$，优化问题可以改写为

为了构造对偶问题，我们引入拉格朗日乘子 $\alpha_i \geq 0$ 和 $\mu_i \geq 0$，拉格朗日函数定义为

令 $\mathcal{L}$ 对 $\boldsymbol{w}$，$b$ 和 $\xi_i$ 的偏导数为零，可得

因此，对偶问题可以表述为

这是一个二次规划问题，我们可以采用梯度下降或者坐标下降等方法求解。

核函数与核技巧

有时候这些样本并不是线性可分的，但是我们可以将它们映射到高维空间，使得它们在高维空间中线性可分。假定映射函数为 $\phi$，则样本 $\boldsymbol{x}_i$ 被映射到 $\phi(\boldsymbol{x}_i)$。我们可以将对偶问题改写为

有趣的是，我们并不需要显式地计算 $\phi(\boldsymbol{x}_i)$，而是通过核函数 $K(\boldsymbol{x}_i, \boldsymbol{x}_j) = \phi(\boldsymbol{x}_i)^T \phi(\boldsymbol{x}_j)$ 来计算内积，因此对偶问题可以改写为

这种方法也称为核技巧（Kernel Trick），下面我们给出几种常用的核函数

核函数 $\kappa(\boldsymbol{x}_i, \boldsymbol{x}_j)$
线性核 $\boldsymbol{x}_i^T \boldsymbol{x}_j$
多项式核 $(\gamma \boldsymbol{x}_i^T \boldsymbol{x}_j + r)^d$
高斯核 $\exp(-\gamma \vert\boldsymbol{x}_i - \boldsymbol{x}_j\vert^2)$
Sigmoid核 $\tanh(\gamma \boldsymbol{x}_i^T \boldsymbol{x}_j + r)$

Platt-SMO算法

Platt-SMO算法来源于坐标下降法，每次只尝试优化一个变量。由于对偶问题中存在约束，我们每次需要优化两个变量。假设我们选择 $\alpha_1$ 和 $\alpha_2$ 来优化，固定其他变量，优化问题可以表述为

其中 $\zeta$ 是一个常数，我们可以将 $\alpha_1$ 表示为

决策函数可以表示为

令 $E_i=f(\boldsymbol{x}_i)-y_i$ 表示预测值与真实值之间的误差。定义辅助变量 $v_1$ 和 $v_2$ 为

于是目标函数可以写成

令 $\mathcal{L}$ 对 $\alpha_2$ 的偏导数为零，可得

令 $\eta = \kappa(\boldsymbol{x}_1, \boldsymbol{x}_1) + \kappa(\boldsymbol{x}_2, \boldsymbol{x}_2) - 2 \kappa(\boldsymbol{x}_1, \boldsymbol{x}_2)$，注意到

于是有

因此

由于存在约束条件 $0 \leq \alpha_1,\alpha_2 \leq C$，因此需要对 $\alpha_2^*$ 进行修剪

其中

于是 $\alpha_1$ 可以通过 $\alpha_2$ 来计算

如果 $0 < \alpha_i < C$，则 $\boldsymbol{x}_i$ 是支持向量，辅助变量 $b_1$ 和 $b_2$ 定义为

因此，偏移量 $b$ 的更新规则为

现在我们已经得到了单次迭代中所有参数的更新公式，我们只需要反复地选择一对 $\alpha_i$ 和 $\alpha_j$ 进行更新，直到收敛为止

算法实现

核函数

我们对上述四种核函数进行实现，这里将核函数封装成类，通过实现__call__方法，使其实例可以像函数一样被调用

  1. 线性核

    1
    2
    3
    4
    5
    6
    class LinearKernel(object):
        def __init__(self):
            self.name = 'linear'
        
        def __call__(self, X, y):
            return X @ y.T

  2. 多项式核

    1
    2
    3
    4
    5
    6
    7
    8
    class PolynomialKernel(object):
        def __init__(self, gamma=1.0, degree=3):
            self.name = 'polynomial'
            self.gamma = gamma
            self.degree = degree
        
        def __call__(self, X, y):
            return np.power(self.gamma * (X @ y.T) + 1, self.degree)

  3. 高斯核

    1
    2
    3
    4
    5
    6
    7
    class GaussianKernel(object):
        def __init__(self, gamma=1.0):
            self.name = 'gaussian'
            self.gamma = gamma
        
        def __call__(self, X, y):
            return np.exp(-self.gamma * np.sum(np.square(X - y), axis=1))

  4. Sigmod核

    1
    2
    3
    4
    5
    6
    7
    8
    class SigmoidKernel(object):
        def __init__(self, gamma=1.0, bias=0.0):
            self.name = 'sigmoid'
            self.gamma = gamma
            self.bias = bias
        
        def __call__(self, X, y):
            return np.tanh(self.gamma * (X @ y.T) + self.bias)

另外，我们定义一个工具函数，方便核函数的创建

1
2
3
4
5
6
7
8
9
10
def CreateKernel(entry):
    if entry['name'] == 'linear':
        return LinearKernel()
    elif entry['name'] == 'polynomial':
        return PolynomialKernel(entry['gamma'], entry['degree'])
    elif entry['name'] == 'gaussian':
        return GaussianKernel(entry['gamma'])
    elif entry['name'] == 'sigmoid':
        return SigmoidKernel(entry['gamma'], entry['bias'])
    raise AttributeError('invalid kernel')

支持向量机

参考scikit-learn的封装，我们定义一个类，提供fit和predict两种方法，参数包括最大迭代次数、惩罚系数、误差精度和核函数类型，利用私有函数实现 $\alpha_i$ 和 $\alpha_j$ 的选择和单步更新，对于线性核，我们提供weight属性，用于获取线性核的分类超平面参数，除了一些简化以外，代码基本按照Platt-SMO算法进行实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
class SupportVectorMachine(object):
    def __init__(self, iteration=100, penalty=1.0, epsilon=1e-6, kernel=None):
        self.iteration = iteration
        self.penalty = penalty
        self.epsilon = epsilon
        if kernel is None:
            kernel = {'name': 'linear'}
        self.kernel = CreateKernel(kernel)
    
    def __compute_w(self):
        return (self.a * self.y) @ self.X

    def __compute_e(self, i):
        return (self.a * self.y) @ self.K[:, i] + self.b - self.y[i]
    
    def __select_j(self, i):
        j = np.random.randint(1, self.m)
        return j if j > i else j - 1
    
    def __step_forward(self, i):
        e_i = self.__compute_e(i)
        if ((self.a[i] > 0) and (e_i * self.y[i] > self.epsilon)) or ((self.a[i] < self.penalty) and (e_i * self.y[i] < -self.epsilon)):
            j = self.__select_j(i)
            e_j = self.__compute_e(j)
            a_i, a_j = np.copy(self.a[i]), np.copy(self.a[j])
            if self.y[i] == self.y[j]:
                L = max(0, a_i + a_j - self.penalty)
                H = min(self.penalty, a_i + a_j)
            else:
                L = max(0, a_j - a_i)
                H = min(self.penalty, self.penalty + a_j - a_i)
            if L == H:
                return False
            d = 2 * self.K[i, j] - self.K[i, i] - self.K[j, j]
            if d >= 0:
                return False
            self.a[j] = np.clip(a_j - self.y[j] * (e_i - e_j) / d, L, H)
            if np.abs(self.a[j] - a_j) < self.epsilon:
                return False
            self.a[i] = a_i + self.y[i] * self.y[j] * (a_j - self.a[j])
            b_i = self.b - e_i - self.y[i] * self.K[i, i] * (self.a[i] - a_i) - self.y[j] * self.K[j, i] * (self.a[j] - a_j)
            b_j = self.b - e_j - self.y[i] * self.K[i, j] * (self.a[i] - a_i) - self.y[j] * self.K[j, j] * (self.a[j] - a_j)
            if 0 < self.a[i] < self.penalty:
                self.b = b_i
            elif 0 < self.a[j] < self.penalty:
                self.b = b_j
            else:
                self.b = (b_i + b_j) / 2
            return True
        return False
    
    def setup(self, X, y):
        self.X, self.y = X, y
        self.m, self.n = X.shape
        self.b = 0.0
        self.a = np.zeros(self.m)
        self.K = np.zeros((self.m, self.m))
        for i in range(self.m):
            self.K[:, i] = self.kernel(X, X[i, :])
    
    def fit(self, X, y):
        self.setup(X, y)
        entire = True
        for _ in range(self.iteration):
            change = 0
            if entire:
                for i in range(self.m):
                    change += self.__step_forward(i)
            else:
                index = np.nonzero((0 < self.a) * (self.a < self.penalty))[0]
                for i in index:
                    change += self.__step_forward(i)
            if entire:
                entire = False
            elif change == 0:
                entire = True

    def predict(self, X):
        m = X.shape[0]
        y = np.zeros(m)
        for i in range(m):
            y[i] = np.sign((self.a * self.y) @ self.kernel(self.X, X[i, :]) + self.b)
        return y
    
    @property
    def weight(self):
        if self.kernel.name != 'linear':
            raise AttributeError('non-linear kernel')
        return self.__compute_w(), self.b

多分类

基于One-Versus-One策略，我们构造 $C_k^2$ 个SVM，其中 $k$ 为类别数，训练每个分类器时，选取相应类别的样本作为训练集，并将标签映射到 $-1$ 和 $1$，在预测时，用每个分类器的预测结果进行投票，从而得到最终结果

我们采用与支持向量机完全相同的封装，提供fit和predict两种方法，使该类成为通用的分类模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class SupportVectorClassifier(object):
    def __init__(self, iteration=100, penalty=1.0, epsilon=1e-6, kernel=None):
        self.iteration = iteration
        self.penalty = penalty
        self.epsilon = epsilon
        self.kernel = kernel
        self.classifier = []

    def __build_model(self, y):
        self.label = np.unique(y)
        for i in range(len(self.label)):
            for j in range(i+1, len(self.label)):
                model = SupportVectorMachine(self.iteration, self.penalty, self.epsilon, self.kernel)
                self.classifier.append((i, j, model))

    def fit(self, X, y):
        self.__build_model(y)
        for i, j, model in tqdm(self.classifier):
            index = np.where((y == self.label[i]) | (y == self.label[j]))[0]
            X_ij, y_ij = X[index], np.where(y[index] == self.label[i], -1, 1)
            model.fit(X_ij, y_ij)
    
    def predict(self, X):
        vote = np.zeros((X.shape[0], len(self.label)))
        for i, j, model in tqdm(self.classifier):
            y = model.predict(X)
            vote[np.where(y == -1)[0], i] += 1
            vote[np.where(y == 1)[0], j] += 1
        return self.label[np.argmax(vote, axis=1)]

性能测试

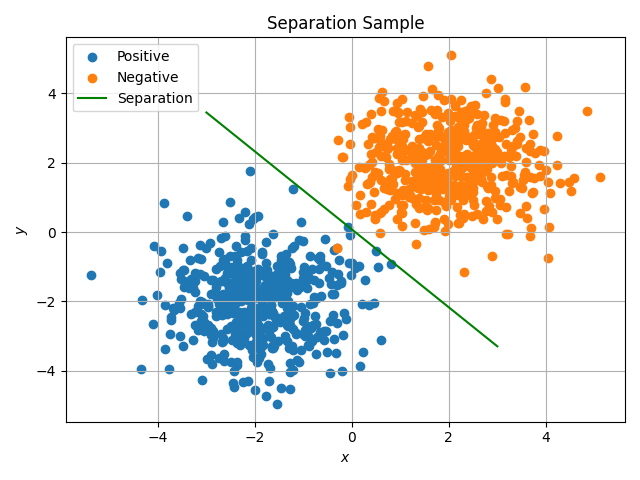
首先，我们在二维平面上构造两组简单的正态分布数据，用于可视化支持向量机的分类效果，首先构造数据并训练模型

1
2
3
4
5
6
7
X = np.concatenate((np.random.randn(500, 2) - 2, np.random.randn(500, 2) + 2))
y = np.concatenate((np.ones(500), -np.ones(500)))
C = SupportVectorMachine(iteration=100)
C.fit(X, y)
w, b = C.weight
u = np.linspace(-3, 3, 100)
v = (-b - w[0] * u) / w[1]

然后根据模型参数绘制分类效果

1
2
3
4
5
6
7
8
9
10
11
plt.scatter(X[:500, 0], X[:500, 1], label='Positive')
plt.scatter(X[500:, 0], X[500:, 1], label='Negative')
plt.plot(u, v, label='Separation', c='g')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.title('Separation Sample')
plt.grid()
plt.legend()
plt.tight_layout()
plt.savefig('./figure/separation.png')
plt.show()

可以看到，我们实现的SVM可以很好地将两组数据分开

为了在MNIST和CIFAR-10数据集上测试性能，需要对数据进行预处理，这里我们将图像展开为向量，并将像素值归一化到 $[0, 1]$ 区间，对于MNIST数据集我们仅保留 $5000$ 个训练样本和 $1000$ 个测试样本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def MNIST(path, group='train'):
    if group == 'train':
        with gzip.open(os.path.join(path, 'train-images-idx3-ubyte.gz'), 'rb') as file:
            image = np.frombuffer(file.read(), np.uint8, offset=16).reshape(-1, 1, 28, 28) / 255.0
        with gzip.open(os.path.join(path, 'train-labels-idx1-ubyte.gz'), 'rb') as file:
            label = np.frombuffer(file.read(), np.uint8, offset=8)
    elif group == 'test':
        with gzip.open(os.path.join(path, 't10k-images-idx3-ubyte.gz'), 'rb') as file:
            image = np.frombuffer(file.read(), np.uint8, offset=16).reshape(-1, 1, 28, 28) / 255.0
        with gzip.open(os.path.join(path, 't10k-labels-idx1-ubyte.gz'), 'rb') as file:
            label = np.frombuffer(file.read(), np.uint8, offset=8)
    remain = 500 if group == 'train' else 100
    image_list, label_list = [], []
    for value in range(10):
        index = np.where(label == value)[0][:remain]
        image_list.append(image[index])
        label_list.append(label[index])
    image, label = np.concatenate(image_list), np.concatenate(label_list)
    index = np.random.permutation(len(label))
    return image[index], label[index]

对于CIFAR10数据集，我们做同样的处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def CIFAR10(path, group='train'):
    if group == 'train':
        image_list, label_list = [], []
        for i in range(1, 6):
            filename = os.path.join(path, 'data_batch_{}'.format(i))
            with open(filename, 'rb') as file:
                data = pickle.load(file, encoding='bytes')
            image_list.append(np.array(data[b'data'], dtype=np.float32).reshape(-1, 3, 32, 32) / 255.0)
            label_list.append(np.array(data[b'labels'], dtype=np.int32))
        image, label = np.concatenate(image_list), np.concatenate(label_list)
    elif group == 'test':
        filename = os.path.join(path, 'test_batch')
        with open(filename, 'rb') as file:
            data = pickle.load(file, encoding='bytes')
        image = np.array(data[b'data'], dtype=np.float32).reshape(-1, 3, 32, 32) / 255.0
        label = np.array(data[b'labels'], dtype=np.int32)
    remain = 500 if group == 'train' else 100
    image_list, label_list = [], []
    for value in range(10):
        index = np.where(label == value)[0][:remain]
        image_list.append(image[index])
        label_list.append(label[index])
    image, label = np.concatenate(image_list), np.concatenate(label_list)
    index = np.random.permutation(len(label))
    return image[index], label[index]

由于CIFAR10数据集较为困难，我们考虑利用CV方法进行特征提取，这里我们使用HOG特征提高分类效果，首先将彩色图像转换为灰度图像

1
2
3
def RGB2Gray(image):
    image = 0.299 * image[0] + 0.587 * image[1] + 0.114 * image[2]
    return image.reshape(1, *image.shape)

然后实现一个简单的HOG特征提取函数，这里我们没有实现区块重叠，对该函数进行改进应该可以进一步提高分类效果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def HOG(image, block=4, partition=8):
    image = RGB2Gray(image).squeeze(axis=0)
    height, width = image.shape
    gradient = np.zeros((2, height, width), dtype=np.float32)
    for i in range(1, height-1):
        for j in range(1, width-1):
            delta_x = image[i, j-1] - image[i, j+1]
            delta_y = image[i+1, j] - image[i-1, j]
            gradient[0, i, j] = np.sqrt(delta_x ** 2 + delta_y ** 2)
            gradient[1, i, j] = np.degrees(np.arctan2(delta_y, delta_x))
            if gradient[1, i, j] < 0:
                gradient[1, i, j] += 180
    unit = 360 / partition
    vertical, horizontal = height // block, width // block
    feature = np.zeros((vertical, horizontal, partition), dtype=np.float32)
    for i in range(vertical):
        for j in range(horizontal):
            for k in range(block):
                for l in range(block):
                    rho = gradient[0, i*block+k, j*block+l]
                    theta = gradient[1, i*block+k, j*block+l]
                    index = int(theta // unit)
                    feature[i, j, index] += rho
            feature[i, j] /= np.linalg.norm(feature[i, j]) + 1e-6
    return feature.reshape(-1)

基于这些工具函数，我们可以优雅地完成图像分类任务，对于MNIST数据集，一个基于线性核的分类示例如下

1
2
3
4
5
6
7
8
9
10
X_train, y_train = MNIST('./dataset/mnist_data/', group='train')
X_test, y_test = MNIST('./dataset/mnist_data/', group='test')
X_train, X_test = X_train.reshape(-1, 28*28), X_test.reshape(-1, 28*28)

model = SupportVectorClassifier(iteration=100, penalty=0.05)
model.fit(X_train, y_train)
p_train, p_test = model.predict(X_train), model.predict(X_test)

r_train, r_test = ComputeAccuracy(p_train, y_train), ComputeAccuracy(p_test, y_test)
print('Kernel: Linear, Train: {:.2%}, Test: {:.2%}'.format(r_train, r_test))

对于CIFAR10数据集，一个基于HOG特征和高斯核的分类示例如下

1
2
3
4
5
6
7
8
9
10
11
X_train, y_train = CIFAR10('./dataset/cifar-10-batches-py/', group='train')
X_test, y_test = CIFAR10('./dataset/cifar-10-batches-py/', group='test')
X_train, X_test = BatchHOG(X_train, partition=16), BatchHOG(X_test, partition=16)

kernel = {'name': 'gaussian', 'gamma': 0.03}
model = SupportVectorClassifier(iteration=100, kernel=kernel)
model.fit(X_train, y_train)
p_train, p_test = model.predict(X_train), model.predict(X_test)

r_train, r_test = ComputeAccuracy(p_train, y_train), ComputeAccuracy(p_test, y_test)
print('Kernel: Gaussian, Train: {:.2%}, Test: {:.2%}'.format(r_train, r_test))

经过测试，我们实现的SVM分类器在MNIST和CIFAR10数据集上的分类精度如下表所示

核函数 组别 MNIST CIFAR10 CIFAR10-HOG
线性核 训练集 96.96% 76.14% 77.58%
测试集 90.70% 33.60% 39.50%
多项式核 训练集 100.00% 99.86% 100.00%
测试集 94.00% 37.70% 44.10%
高斯核 训练集 99.68% 99.14% 94.54%
测试集 94.80% 34.10% 47.00%
Sigmoid核 训练集 95.42% 7.96% 59.82%
测试集 92.10% 7.40% 44.70%

此外，我们对模型的收敛性和各个核函数的参数选择进行了测试，模型精度与迭代次数的关系如下图所示

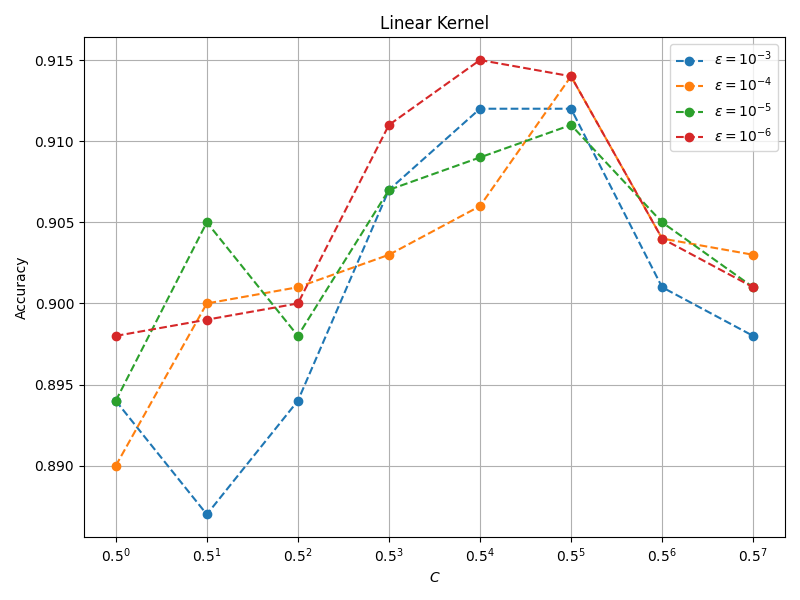
线性核分类精度与 $C$ 和 $\varepsilon$ 的关系如下图所示

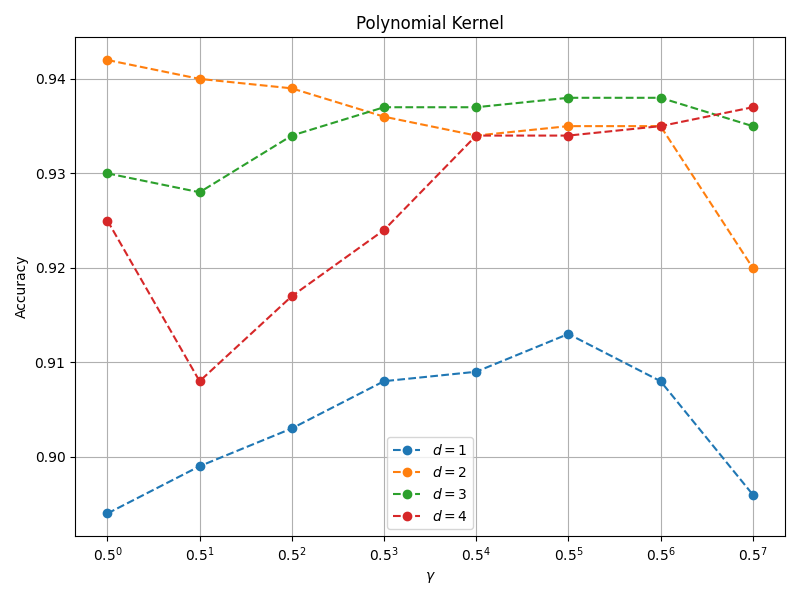
多项式核分类精度与 $\gamma$ 和 $d$ 的关系如下图所示

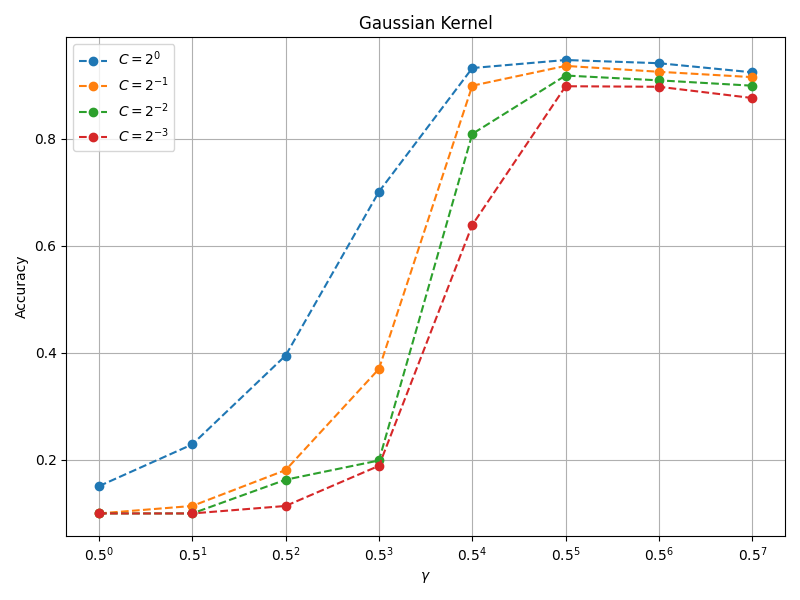
高斯核分类精度与 $C$ 和 $\gamma$ 的关系如下图所示

Sigmoid核分类精度与 $\gamma$ 和 $r$ 的关系如下图所示

上述结果揭示了各个参数对模型性能的影响，可以为调参提供一定的指导作用

写在最后

SVM从过去的炙手可热到如今的日薄西山，仅仅过去了十年的时间，无论是精度还是效率，SVM都完败于当下随处可见的神经网络，关于从零开始实现SVM的意义，我也感到迷茫，但这一过程或多或少改变了我对机器学习的认知，一个简洁优雅的多项式时间精确算法，也许只能满足理论研究者的洁癖，而优化复杂模型的近似算法，在工程上赢得了未来。作为一门课程的大作业，笔者的实现难免存在疏漏和不足，希望读者谅解